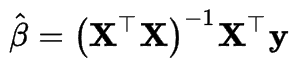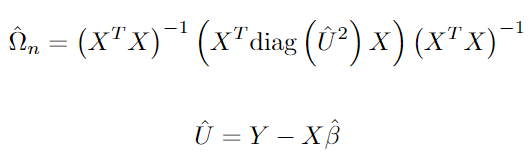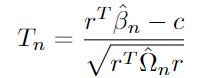MODULE 2.1
READING:
swirl: Module 2
Task:
Download the task folder. Use the R script in the /script subfolder. Load the task dataset AER 2000-2022.csv by referencing the correct directory. Do not shift files around to accomplish this. You may add lines of code in the R script as you see fit.
Load the QJE 2000-2022.RData file.
Look at the aer and qje databases, specifically paying attention to the id, title, and author_names variables.
Now, run the code enclosed by the DO NOT EDIT (Part 4) comments. The aer and qje databases are manipulated. Look at the aer and qje databases again after running lines 20 to 24. What happened? (Hint: Pay attention to the id, title, and author_names variables)
Let’s find out which authors have published in both AER and QJE within the database’s timeframe. Run the code enclosed by the DO NOT EDIT (Part 5) comments. What is the resulting dataframe like? Comment briefly. Do you recognize some of these economists?
Save the resulting dataframe as a .txt file in a subfolder called Results, separating by line. (Hint: “\n” is line break.)
Submit the folder R_Beginner_2 in a .zip or .7z compressed file.
(You do not need to submit the exercise in Chp 9.9 of YaRrr)
MODULE 2.2
READING:
Causality and Econometrics, Heckman and Pinto (Section 2.1-2.2)
Causal Analysis After Haavelmo (Section 2, up to first paragraph on pg 119; access is provided by UChicago library)
YaRrr Chp 16.3 (Watch the video below and ignore references to functions for now)
P-Set 2
Remember to document your code well. Report all results in a LaTeX-rendered PDF document. Submit your .R file and your .PDF file in a single compressed folder (.7z, .zip, or .rar).
TASK:
In this problem set, we will recreate the OLS (ordinary-least-squares) estimator that is used in most regressions in economics. You’re basically recreating part of the function lm(). You may not load any library for this problem set.
Problem 1
Describe what a linear regression is.
Problem 2
Describe what the OLS estimator is.
Problem 3
Under what assumptions can we interpret a simple OLS linear regression causally?
Problem 4
Download two artificially-generated databases on student test scores here and here. Import them in R as test_early and test respectively.
Problem 5
View the databases. A school in a nearby district has sent the test scores of math, reading, and science exams for their third grade to us. The databases also contain some demographic information about the students. We wish to investigate the impact of various characteristics on math test scores and do a linear regression. What is the y-variable (dependent variable) of interest in test_early? Create the vector y as the observations of the y-variable.
Problem 6
What are the four x-variables of test_early? Create the matrix x as that. Also include an intercept variable (i.e., a vector of 1s). Ensure that the matrix is such that each observation is its own row. The final matrix should be 1218 (rows) by 5 (columns) (1218 observations of 5 variables).
Problem 7
The OLS estimator on the observed data is the following:
Construct the OLS estimator of this data and assign it to beta. Hint: inverse, transpose, matrix multiplication.
Problem 8
What is the coefficient of family income? Print it directly by referencing the correct index of beta. Hint: which index is family income in X? Verify that this is correct using the lm() command.
Problem 9
Create y_sub consisting of only the first 600 observations in y. Create x_sub consisting of only the first 600 observations in x.
Problem 10
Once again construct the OLS estimator of this subsample and assign it to beta_sub. What is the coefficient of family income now? Print it.
Problem 11
The heteroskedasticity-robust estimator, omega, of the covariance matrix of beta is the following:
Note that the square of the vector U is not the matrix of multiplication of U on itself but rather the square of all its components. We then want a diagonal matrix constructed based on the square of the vector U. Hint: You will need to first force U squared into a vector with as.vector().
Construct this estimator based on the full sample and assign it to omega. Hint: diagonal. Omega should be a 5-by-5 matrix.
Problem 12
The test statistic, T, of the null hypothesis c is the following:
Here, r can be thought of as the selection vector: if the j-th component of r is 1 and all other components of r is 0, then r’ beta is the j-th component of beta. r should have a length equal to the length of beta.
c is the null hypothesis we wish to test. This should be a scalar (i.e. a single number).
n is the number of observations of the data.
Construct the test statistic of the null hypothesis that the effect due to IQ is 0. Assign this to t-stat. Ensure that the final result is a single vector instead of a 1 by 1 matrix. Hint: use as.vector().
Problem 13
The p-value of the test statistic for a single hypothesis is given by the following:
Here, Phi is the standard normal CDF. In R, this function is pnorm. Construct the p-value of the test statistic generated in Problem 12. Assign this to p. Is the coefficient for IQ statistically significant? Hint: absolute values.
Problem 14
Repeat the process above and find the p-value for ADHD, this time using the test database and using science test scores. Is the coefficient for ADHD statistically significant? Verify that your results are accurate with the following code:
library(lmtest)
library(sandwich)
lmfit = lm(Science ~ Family_income + Teacher_postgrad_educ + Teacher_exp + IQ + ADHD,
data=test)
coeftest(lmfit, vcov = vcovHC(lmfit))The lmtest and sandwich packages provide implementations for heteroskedasticity-robust standard errors linear regressions. You may encounter these in your econometrics class.
Problem 15
Under what conditions can we say that ADHD has a statistically significant causal effect on test scores? Is this verifiable from the data alone?